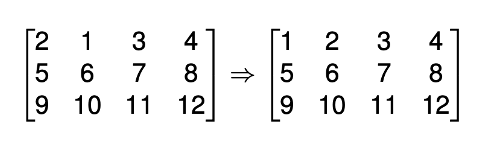コマを縦横に動かすことで与えられた盤面のコマの配置を変更することができるであろうか?1878年にパズル作家のサム・ロイドによって「15パズルで14のコマと15のコマ を入れ替えた状態を元の状態に戻す」ことが出題された。
サム・ロイドの15パズルとは以下の質問です。
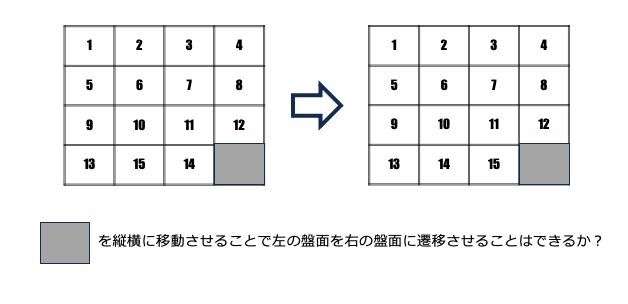
実はこれは不可能なことである。何かが可能であることは、それを実際にやってみせることで証明することができる。ところが何かが不可能であることを証明するには、多くの試みが失敗に終わることを示しただけでは十分ではない。何かが不可能であることを証明するにはどうすればいいのだろうか?現代数学には不可能性の証明と呼ばれるものいくつかがある。15パズルの状態遷移が可能ではないケースもあることを証明するにも、対称群と交代群と呼ばれる現代数学の基本的な概念を活用して証明することができる。
2次元配列の左端の行の塊や上部の列の塊を反転させることで2次元配列の配置を遷移させることはできるでしょうか?次のようなケースでは緑色の四角で囲まれた部分を反転することで左端の配列を右端の配列に遷移させることが可能です。マイクロソフトの共同創業者であるビル・ゲイツが取り組んだパンケーキソート問題を高次元に拡張した研究課題です。例えば、以下のように2次元配列の状態遷移が可能です。

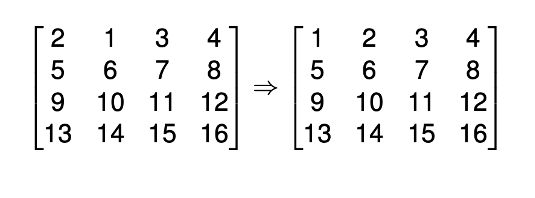
それでは同様に左端の行の塊や上部の列の塊を反転させることで次の二つの2次元配列の配置を遷移させることはできるのでしょうか?群や亜群(Groupoid)と呼ばれる概念を利用することで(1)の遷移は可能であり、(2)の遷移は不可能であることを証明しました(論文1、論文2)。代数系(群、亜群)を活用して不可能性を証明することの具体例です。