研究分野は代数学、組合せ数学、コンピュータサイエンス、ロジック、情報セキュリティとなり、数学と情報学基礎に広範囲にわたります。 これらの研究の根底には、数学的な構造とそれに関わるアリゴリズムを解析するという共通の目標があります。 特に、代数系（群、半群、亜群）の構造の解析と関連するアルゴリズムに興味を持っていて、実社会に役立つ暗号技術やオートマトンに応用しています。
群・半群・亜群
群、半群（特に逆半群）、亜群（Groupoid）の有限表示と代数的構造の解明、そして、関連する語の問題やその他のアルゴリズム問題に取り組んでいます。無限群や無限半群は構造が分かりにくいものですが、幾何学的な構造を利用することで効率的なアルゴリズムを構築することが出来る場合があります。自由積、融合積、HNN拡大などの組合せ群論・幾何学群論における重要概念とBass -Serre理論との関連に興味を持っています。（論文１、論文２、論文３、論文４）
グラフや組合せ構造を用いた手法だけでなくvan Kampen ダイアグラムと呼ばれる幾何学的手法を用いることでアルゴリズム問題の可解性・決定性やその計算効率を研究しています。アルゴリズム問題の可解性・決定性はロジック（数理論理学）の研究分野でもあり、代数学、論理学、グラフ理論など多様な手法を駆使する研究となります。（論文５、論文６）
逆半群と亜群による局所的な対称性と偏作用は数学において様々な応用がありますが、群の作用と比べるとはるかに難しいものですが、研究対象として最も興味を持っています。結晶構造は群によって規定できますが、ペンローズタイリングのような構造の解析に群は適しません。代数系に幾つかの応用を発見しています。（論文７）
オートマトンと形式言語理論
代数学、離散数学、グラフ理論と強い関連を持つのがコンピュータサイエンスの研究です。チューリングマシンやオートマトンといった構造は計算機の理論的モデルとして活用さえています。形式言語理論はプログラミング言語などの機械語をモデル化することに役立つ理論です。オートマトンは受理できる言語の豊富さによりその能力が決まります。
有限オートマトンやプシュダウンオートマトンの読み取りヘッドの振る舞いを変更することで言語受理能力がどのように影響を与えるのか興味を持っており、一方向性ジャンピングオートマトンの概念を提案して解析しています。（論文８、論文９、論文１０）
離散数学
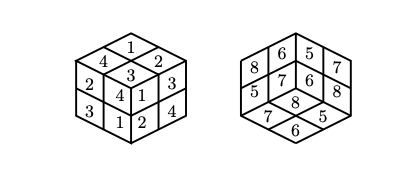
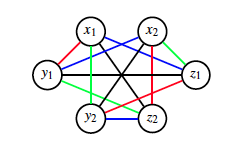
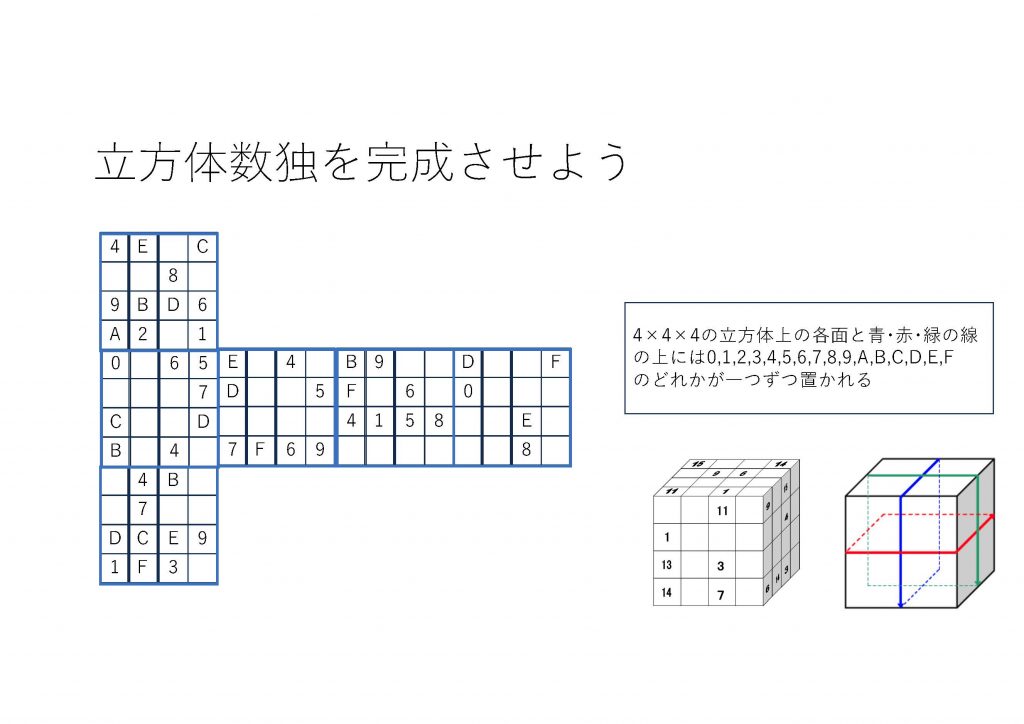
組合せ構造の研究として、ラテン立方体と正則3部グラフと関連する組合わせデザインの関係を調べています。正則3部グラフが完全1-因子分解を持つケースを解析しています。2次のラテン方陣の総数を計算機実験で求める研究も実施しています。ラテン立方体はラテン方陣を立方体の表面に拡張したものです。ラテン立方体を基に数独のようなパズルを作る事もできます。（論文１１）
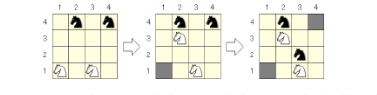
立方体上の組み合わせ構造を調査する研究は８クイーン問題を立方体上に拡張することから始まりました。８クイーン問題とは、チェスの盤上に、８個のクイーンをどのコマも互いに当たりがない配置を求めることである。nクイーン問題とnルーク問題を立方体上で考察しました（論分１２）。群論のCauchy-Frobeniusの定理を応用しています。
また15パズルにおいて群の作用が解決の鍵となりますが、パンケーキソート問題を2次元に拡張した際には群ではなく亜群の偏作用の概念が必要になります。亜群と偏作用の概念の理解を目的とした研究も大きなテーマの一つです。
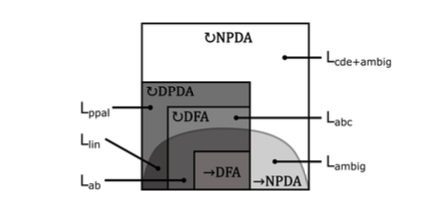
アルゴリズム
組合せ最適化問題を解決する群知能の研究も行っています。アリやハチなどの自然界の生物群の群行動を模倣した群知能を使うことで厳密な解を求めることが難しい組合せ最適化問題の近似解を効率良く求める研究です。群知能は人工知能の一つの分野と認識されていて、様々な組合せ最適化問題に応用されています。ハチやホタルの集団行動を模したアルゴリズムを施設配置問題に応用しました。（論文１３、論文１４）
将棋や囲碁などのゲームではAIが人の能力を超えて強力になっています。対戦ゲームの理論では、モンテカルロ木探索という手法を用いて盤上ゲームにおける対戦プレイヤーをプログラムする研究も行っています。Knight-Amazon という盤上ゲームを提案し、必勝戦略が存在するケースを解明しました。（論文１５、論文１６）
情報セキュリティ
暗号、認証技術の研究として、公開鍵暗号や暗号プロトコルの研究を行っています。特に、公開鍵暗号の基礎とする整数論、代数学、離散数学に関連する数学構造とそのアルゴリズム問題に興味を持っています。準同型暗号の代数学的な構造を解析し代数構造とアルゴリズムの問題との関連に興味を持っています。（論文１７、論文１８、論文１９）
量子コンピュータのセキュリティへの影響についても研究しています。（論文２０）
また匿名性を有する認証方法や秘密を保持したままのデータベース検索などの暗号プロトコルの安全性や設計手法、安全性解析についても興味があり、有限群に関する部分群メンバーシップ問題を利用した暗号プロトコルや準同型暗号の構成や安全性を研究しています。安全・安心な情報通信ネットワーク社会を実現するには公開鍵暗号や暗号プロトコルが不可欠です。（論文２１、論文２２、論文２３、論文２４）
ブロックチェーン
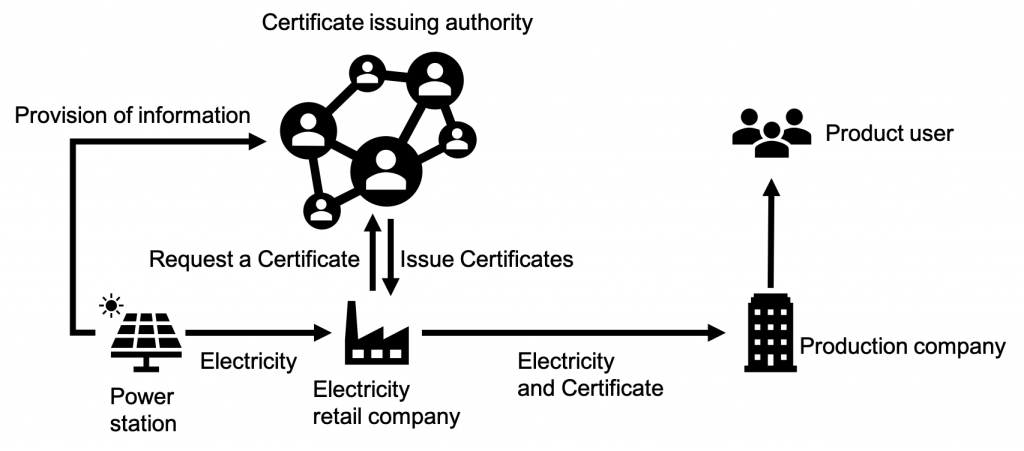
非中央集権化を目的とするブロックチェーンは仮想通貨などにも応用されており、暗号技術（電子署名、ハッシュ関数など）を利用しています。これからの経済活動において重要となる技術です。ブロックチェーンを（CO2などの温室効果ガスを排出しない再生可能エネルギーによって発電されたことを保証する）再生可能エネルギーの証明書に活用する研究を行っています。（論文２５）
