研究背景
電子が量子力学的な粒子(量子)であることの特徴の一つとして、固体結晶などの周期構造中に現れるエネルギー分布のバンド構造(エネルギースペクトルにおける禁制帯の存在)が挙げられます。このバンド構造は、電子の存在確率が波動として振る舞うことによって生じ、電子を単なる帯電した古典的な粒子として捉えるだけでは、その本質を理解できないことを示しています。この特性は固体物理学において深く研究され、半導体工学などにおける応用研究を経て、現在では身の回りの機器で広く活用されています。物質設計や微細加工技術のさらなる進歩に伴い、より巧妙に量子力学的効果(量子効果)を利用したデバイスの開発も進んでいます。
上述の波動性に起因する特性に加え、電子の特徴としてスピン角運動量(スピン)と呼ばれる自由度も知られています。電子のスピンは古典的な自転運動に類似していますが、決して停止することはなく、電子の大きさが現在の技術では特定できないほど小さいことを考慮すると、純粋に量子力学的な特性と考えられます。スピンの自由度により電子は小さな磁石として振る舞い、物質の磁気的な性質(磁性)の担い手にもなります。さらに、スピンが電気伝導などの輸送現象に及ぼす効果や、逆に輸送現象がスピン由来の磁性に及ぼす効果も発見されており、これらを応用した分野も急速に発展しています。


以上の経緯により、固体中の電子をより深く理解し、新たな活用法を探求するためには、スピン自由度を持つ波動の理解が不可欠であると考えられています。スピンのような内部自由度を持つ波動には、Berry位相と呼ばれる幾何学的な位相が現れることが知られており、特にスピンと軌道運動の結合が無視できない系では、この位相の効果が輸送現象に顕著に現れることが分かっています。
話は少しそれますが、私たちの日常生活に欠かせないもう一つの重要な量子として光子があります。視覚に必要な可視光をはじめ、ワイヤレス通信に用いられる電波や赤外線、レントゲン撮影に使われるX線、そして放射線の一種であるガンマ線はいずれも電磁波の一種であり、光子の集まりと考えられています。光子もスピンの自由度を持っており、電磁波の偏光の自由度と直接関係しています。そのため、電子と同様に、幾何学的位相に起因する興味深い現象を示すことが期待されます。例えば、空気と水の界面で光線が屈折してその進行方向が変化する際、入射光の方向および屈折による変化の方向のいずれにも垂直な方向に、入射光の偏光状態に依存した屈折後の光線の横ズレが生じる現象があります。この現象は、後述する電子系におけるスピンHall効果の光子系における類似現象として理解することができます。
当研究室では、主に固体中の電子系におけるスピン自由度の影響が顕著な輸送現象や、周期構造中の光子系なども含め、内部自由度を伴う波動の幾何学的位相に起因する現象について研究しています。また、そのような現象を探索するために必要な模型や解析手法の考案も行っています。以下では、これまでに行った主な研究テーマを紹介します。
研究内容
異常Hall効果の幾何学的側面と不純物散乱局在効果によるHall伝導率の量子化
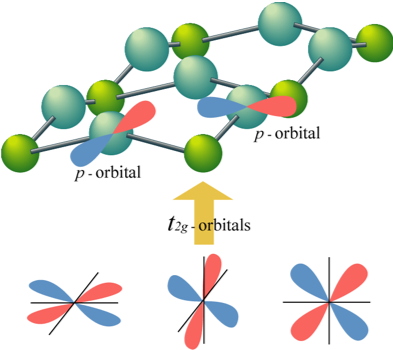
伝導体に磁場をかけた状態で電流を流すと、電流と磁場の両方に垂直な方向に起電力が生じる現象をHall効果と呼びます。また、強磁性金属では外部磁場だけでなく、磁化に依存した同様の現象も観測され、これを区別して異常Hall効果と呼びます。異常Hall効果が生じる仕組みには、電子に対するスピン依存散乱による外因的機構と、エネルギーバンドを形成する電子状態の特殊性に起因する内因的機構があります。いずれの機構においても、スピン軌道相互作用が重要な役割を担っています。
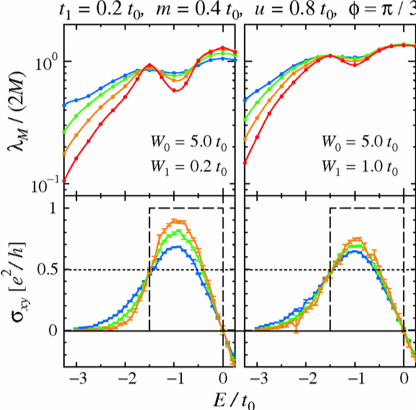
ここでは内因的機構に注目し、電子状態の特殊性を幾何学的位相の概念を通じて理解することで、この機構がより効果的に働くための条件を明らかにしました。この知見は物質設計において重要な指針となり得ます。また、不純物散乱による局在効果により、電子のエネルギーバンド全体の持つ位相幾何学的な特性が顕在化し、強磁場中の2次元電子系における量子Hall効果と同様の仕組みで、2次元強磁性金属においてもHall伝導率の量子化が起こり得ることを理論的に示しました。
スピンHall効果および量子スピンHall効果におけるスピン流・スピン蓄積と不純物による局在効果
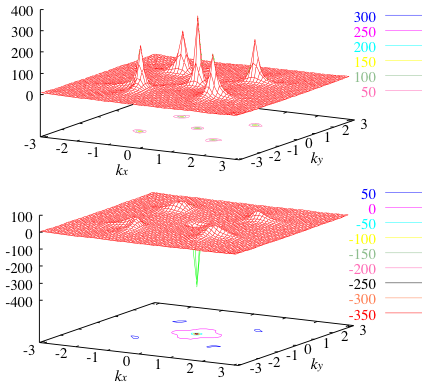
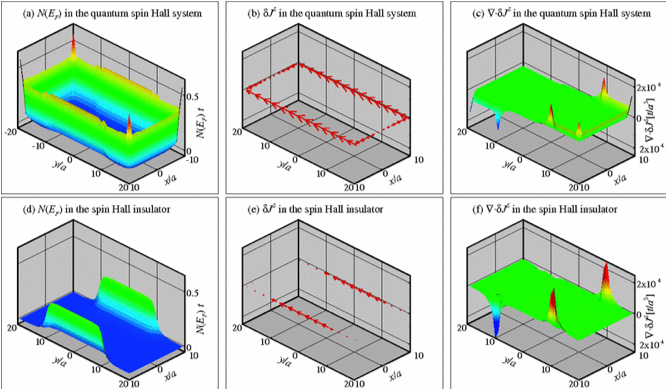
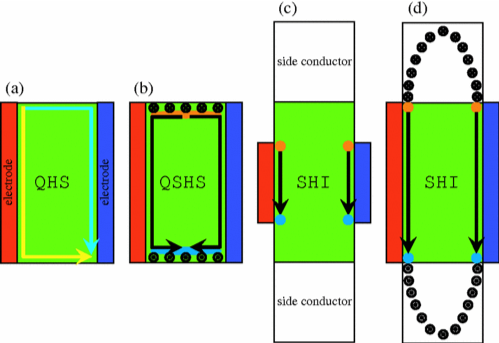
前述のように、電子は電荷のほかにも、自転運動に類似したスピンと呼ばれる自由度を持っています。スピンHall効果とは、表面的にはHall効果における電荷をスピンに置き換えたような現象として現れ、電流と直交する方向にスピン蓄積が生じるというものです。さらに、量子Hall効果に対応する現象として量子スピンHall効果が知られており、スピンHall効果と同様にスピン軌道相互作用が重要な働きをします。スピン軌道相互作用のため、スピンは電荷と異なり保存量ではなく、スピンHall伝導率とスピン蓄積の関係は、Hall伝導率とHall起電力の関係よりもずっと複雑なものとなります。そこで、非平衡定常状態における実空間シミュレーションを用いて、有限系のスピンHall効果・量子スピンHall効果におけるスピン流とスピン蓄積の様子を明らかにしました。
量子スピンHall効果は量子Hall効果と同様に特殊なエッジ状態の存在を示唆しており、その存在はバルク状態の位相幾何学的な非自明性と関連しています。量子Hall効果の場合には、この非自明性が不純物散乱による局在効果において顕著に現れることが知られています。このことを踏まえ、量子スピンHall効果に対する不純物の影響を解析し、量子Hall効果や通常のスピンHall効果における局在効果との違いを明らかにしました。
光の幾何学的Hall効果と光カイラルエッジモード
電子系における内因的機構による異常Hall効果やスピンHall効果の本質は、量子である電子が持つ波動性に伴う幾何学的位相にありました。この位相が現れる条件の一つとして、スピンと軌道運動の結合が挙げられます。光子の集まりである電磁波が持つ偏光の自由度は光子のスピン自由度と対応しており、また、光子は質量を持たない相対論的な粒子のため、スピンと軌道運動が強く結合しています。そこで電子系における知見をもとに、古くから知られていた光線の反射・屈折における横ズレが、内因的機構による光のスピンHall効果として理解できることを明らかにしました。さらに、屈折率が周期的に変調したフォトニック結晶と呼ばれる人工結晶中を伝搬する電磁波に対する同様の効果を理論的に示しました。
前述のことは、スピン角運動量に代わる内部軌道角運動量を持った電磁波を周期構造を用いて生成できることを意味し、さらに、このような電磁波が位相幾何学的に非自明な幾何学的位相を持ち得ることを示しています。電子系の量子Hall効果に現れるカイラルエッジ状態の光子系版を磁性フォトニック結晶において実現できることが、海外のグループにより示されました。このことを受け、理論模型を用いて光カイラルエッジモードについて詳しく調べ、試料のエッジに沿って閉じ込められた本物の光カイラルエッジモード以外にも、光子系に特有の外部への漏れを伴う共鳴的な光カイラルエッジモードも存在することを明らかにしました。また、これらのモードをうまくつなげることで後者を通じて外部から前者を励起できることを示しました。
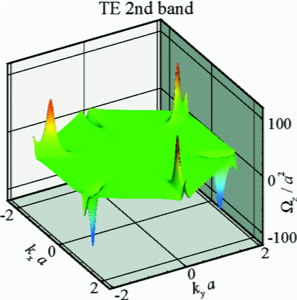
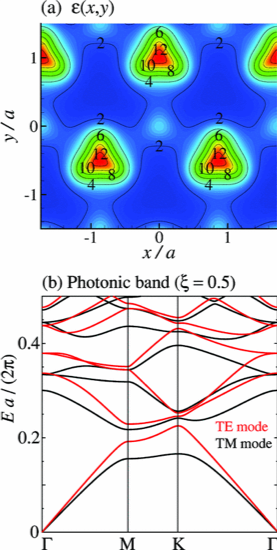
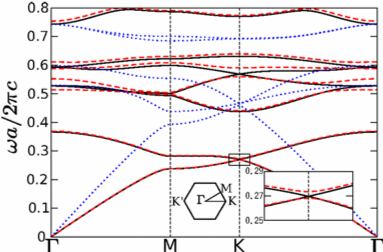
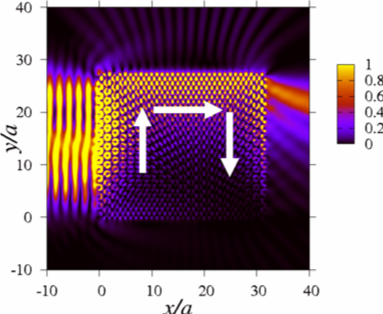
環状渦構造をもつトロイダル光波束の伝搬特性
電磁波のもつ偏光の自由度は光子のスピン角運動量に由来しており、古典的な通信における多重化や量子情報通信における量子ビットの実装に利用されています。これらの成功例において共通するのは、狭い周波数帯における複数のほぼ直交するモードの利用です。一方、電磁波は軌道角運動量をもつこともでき、スピン角運動量の自由度を補完するものとして期待されています。同様の考え方のさらなる拡張を探求することは意義深いと考えます。
また、微細加工技術の進歩により、電磁モードの位相幾何学的特性を利用した新しいタイプのフォトニック材料の設計が可能になりました。フォトニック結晶における光子系版の幾何学的ホール効果や量子ホール効果、結晶トポロジカル絶縁体などが提案され、そのいくつかは実現されています。
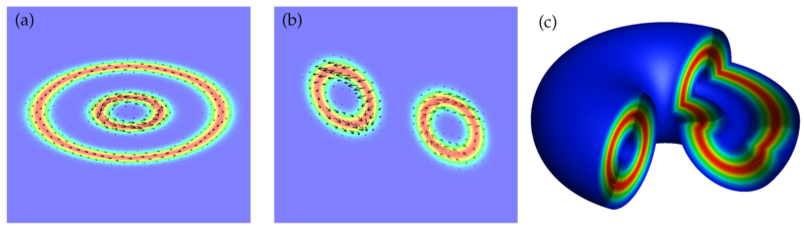
以上の進展に着想を得て、軌道角運動量に関連した線状の渦だけでなく、環状の渦を持つ新しいトロイダル光波束の可能性を提案しました。生成方法の一つの案として、光子系版結晶トポロジカル絶縁体の表面の利用が考えられますが、まだ十分な検証はできていません。ここではまずその伝搬特性を数値的に調べるために、複数の種類の渦を持つMaxwell方程式の解を構築するための簡単なアルゴリズムを示しました。さらに、均質な誘電体間の界面における反射と屈折に対するそのような波束の安定性や、渦の構造に見られる位相幾何学的な特性が、反射や屈折を通じてどのように変換するのかを明らかにしました。


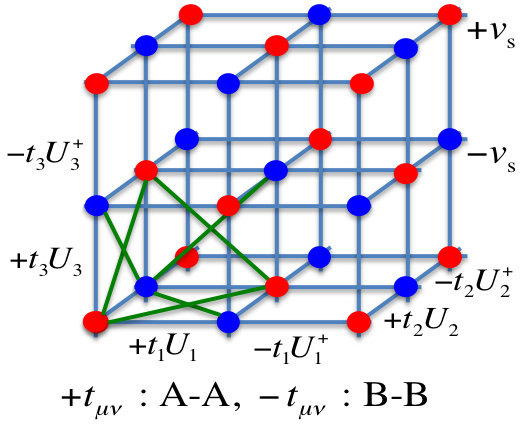
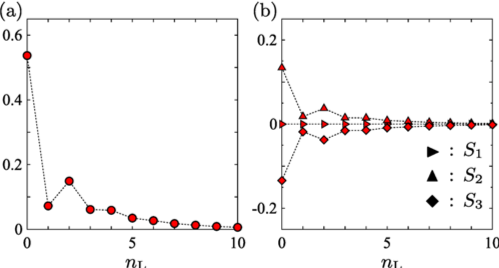
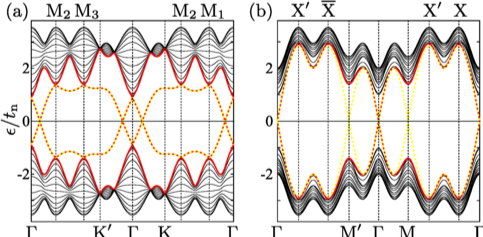
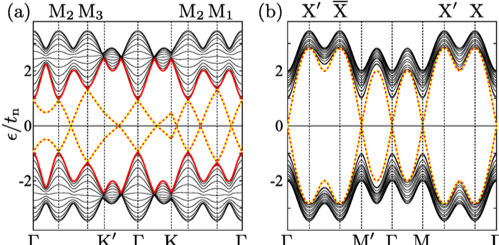
トポロジカル表面状態の厳密解をもつ格子模型の系列
位相幾何学的に非自明な特性を備えた人工量子系の設計が可能となりつつある状況を踏まえ、トポロジカルな表面・界面が関係したユニークなダイナミクスを解析するためのツールの提供を目指し、表面状態まで含め解析的に解くことができる格子模型の系列を考案しました。表面状態の解はその形に対してある仮説を課し、解析的に構成することで導出されます。こうして得られた解は有限系では近似的なものですが、半無限系では厳密解となるものです。
解析解の構成には最近接ホッピングに対するある種の制限を利用しています。ただし、この制限にもかかわらず様々なタイプの表面状態を記述できるだけの十分な設計性を備えた模型の系列になっています。トポロジカル絶縁体、非トポロジカル絶縁体、それらの境界に対応する模型について、いくつかの異なる方向の表面に対する解析解を具体的に導出し、十分な大きさの有限系に対する数値解と比較することで、エネルギー分散、電荷分布、スピン分布のいずれに関しても極めてよく記述できることを示しました。